¿Qué es la probabilidad?
La probabilidad es una predicción matemática de que algo va a ocurrir y se suele expresar con un número entre 0 y 1 o en porcentajes del 0% al 100%.
En esas representaciones un suceso con un 0% de posibilidades de ocurrir es un suceso imposible, y un suceso con un 100% de posibilidades de ocurrir, un suceso seguro. Vamos a entender el concepto de la probabilidad mediante varios ejemplos:

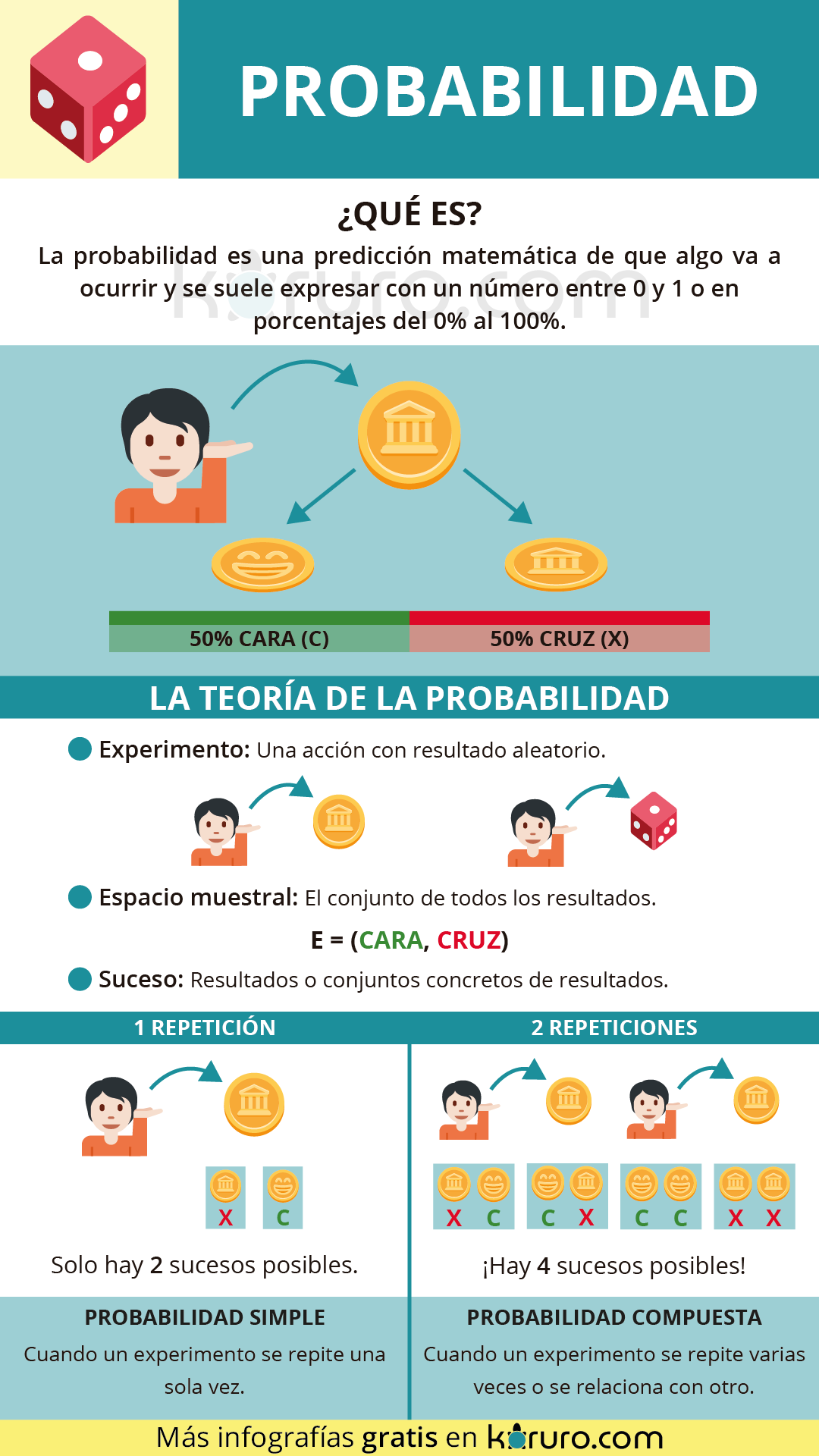
Imagina que tienes una moneda en tus manos. Si la tiras al aire, siempre caerá de uno de sus lados, por lo que la probabilidad de que, lanzando la moneda, salga cara, es del 50%, y la posibilidad de que salga cruz, del 50% también.
Si un genio te dijera que te va a dar mucho dinero si adivinas de qué lado va a caer la moneda, daría igual por qué lado apostar, ya que ambos lados tienen la misma probabilidad de salir.
Imaginemos que el pronóstico del tiempo dice que hay un 95% de probabilidades de que llueva mañana ¿Eso quiere decir que mañana lloverá?
Pues lo más probable es que sí, pero puede que no. El resultado no lo sabremos hasta mañana.
Al tirar una moneda al aire, como hemos dicho, la probabilidad de que salga cara es un 50% ¿Por lo que si tiro una moneda al aire 100 veces, conseguiré cara 50 veces y cruz otras 50, verdad?
NO. Los únicos porcentajes que expresan certeza son el 0% y el 100%. Yo mismo he hecho este experimento y en 100 tiradas me ha salido:
Cara: 45 veces
Cruz: 55 veces
Teóricamente, debería haber logrado cara 50 veces y cruz otras 50, pero no ha sido así. Eso es porque la probabilidad se basa en la predicción, y, por tanto, aunque la probabilidad prediga algo, luego puede ocurrir cualquier cosa.
Aplicaciones de la probabilidad en la vida real
Como habrás podido ver mediante los anteriores ejemplos, gracias a la posibilidad podemos saber con cierta certeza si algo ocurrirá en el futuro. Y todo esto tiene muchas aplicaciones en nuestro día a día, como, por ejemplo:
- En la meteorología, para saber qué tiempo hará. Esto es muy simple: los meteorólogos utilizan grandes bases de datos para estimar qué probabilidad hay de que haga cierto tiempo en un sitio ¡Y cada vez aciertan más!
- En los casinos, para ganar dinero, ¿Alguna vez has visto la típica ruleta sobre la que se tira una bola? Tiene dos colores: rojo y negro. Y tú apuestas en qué color caera la bola: si aciertas duplicas lo apostado, y, si fallas, lo pierdes. Pues bien: aquí el único que gana es el casino, porque hay también una casilla blanca que hace que tú ya no tengas un 50% de posibilidades de acertar.
- Para determinar las condiciones de los seguros. Imagínate que vas a contratar un seguro de coche y eres joven. Pues probablemente te tocará pagar más que lo que pagará una persona mayor. Y eso es así porque las compañías de seguros estiman que la probabilidad de que tengas accidentes es mayor que la de una persona con más edad ¡Aunque luego tu puedas ser un excelente conductor!
- Para medir la efectividad de las vacunas. Las vacunas se prueban en grupos de muestra antes de ser lanzadas al mercado, para estimar qué efectividad pueden tener. De esa forma, cuando una vacuna tiene una probabilidad elevada de protegerte contra un virus, es lanzada al mercado.
- Y, al fin y al cabo, ¡En cualquier acción de tu día a día! Así es. Tal vez no calcules probabilidades de forma numérica cada día, pero, por ejemplo, cuando haces un examen piensas en tu probabilidad de aprobar. O cuando llueve y saltas por encima de un charco también pasa por tu cabeza la probabilidad de resbalarte...
La teoría de la probabilidad
La teoría de la probabilidad es el estudio de sucesos aleatorios y consiste en analizar dichos sucesos para determinar si un suceso es más probable que otro. Es, al fin y al cabo, la teoría matemática mediante la que calculamos las probabilidades.
Tiene 3 principales elementos, y lo mejor para entenderla es comprenderlos mediante ejemplos:
| Explicación | Ejemplo |
|---|---|
| Experimento: hacer una acción que puede dar un resultado aleatorio | Imagínate que tiramos una moneda al aire. Puedes obtener cara o cruz de forma aleatoria. Por lo que el hecho de lanzar una moneda y ver qué da es un experimento. |
| Espacio muestral: es el conjunto de todos los posibles resultados de un experimento. Se suele representar con la letra E. | Al lanzar la moneda, solo podemos conseguir cara o cruz. Por lo que el espacio muestral del experimento es: E = (cara ; cruz) |
| Suceso: se denomina suceso al conjunto de posibles resultados de un experimento. | Antes hemos lanzado la moneda una vez y hemos conseguido el suceso cara. Solo había dos sucesos posibles:
|
Como hemos mencionado, esta teoría mencionada sirve para calcular probabilidades y ver, así, usando el lenguaje matemático, cuál es la probabilidad de que cada suceso ocurra. Por ejemplo:
¿Qué probabilidades hay de que, lanzando una moneda al aire 5 veces, consigamos cara 5 veces seguidas?
Sabemos que sacar cara 5 veces seguidas es algo poco probable, pero posible: sabemos que puede ocurrir ¡Pero es muy difícil! Pues para saber con exactitud cómo de difícil es que eso ocurra, se usa el cálculo de probabilidad.
Cuando un experimento se repite una vez (como lanzar una moneda al aire y ver qué sale), las probabilidades de sus sucesos se calculan mediante probabilidad simple.
Si, en cambio, un experimento se repite varias veces o se relaciona un experimento con otro (lanzar la moneda al aire varias veces), las probabilidades de sus sucesos se calculan mediante probabilidad compuesta.
Cada tipo de probabilidad tiene sus fórmulas, y las tienes explicadas en sus respectivos artículos 😉.