¿Qué es?
El Teorema de Pitágoras es una afirmación demostrable que relaciona los lados de los triángulos rectángulos, que son aquellos que tienen un ángulo de 90º. Es utilizado, principalmente, para calcular el valor del lado desconocido de un triángulo en base a otros dos lados conocidos.
Para aplicarlo, es necesario identificar los lados del triángulo rectángulo con los siguientes nombres: hipotenusa, cateto y cateto.

La hipotenusa será siempre el lado más largo, y los otros dos lados serán llamados catetos. Otra forma de nombrarlos es identificar el ángulo recto; una vez identificado, los catetos son los lados que forman ese ángulo recto, y, la hipotenusa, el lado restante.
Una vez nombrados los lados, el teorema dice así:
O, lo que es lo mismo, si llamamos a la hipotenusa a, y a los catetos b y c, obtenemos la fórmula del teorema de Pitágoras, que es la siguiente:
¿Para qué sirve la tesis de Pitágoras?
El teorema tiene aplicaciones en muchos ámbitos de la vida cotidiana, y, se usa, principalmente, para calcular un lado de un triángulo que no conocemos.
Imaginad que queremos calcular cuál es el tamaño de la pantalla de nuestro móvil. Esa medida suele decirse en pulgadas, pero nosotros vamos a calcularla en centímetros. Mediante la proposición de Pitágoras, lo haríamos así:
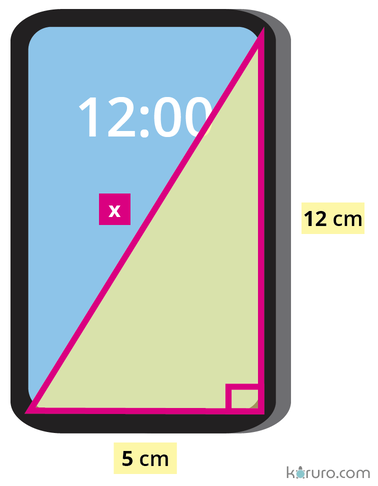
La diagonal del teléfono forma un triángulo con los lados, que miden 12 cm y 5 cm:
- La diagonal es la hipotenusa, porque es el lado más largo del triángulo. Como no sabemos su longitud, lo hemos llamado x.
- Y como ya hemos identificado la hipotenusa, los otros dos lados son los catetos, a los que hemos llamado b y c, y tenemos su longitud: b = 5 cm y c = 12 cm.
Ahora vamos a aplicar el Teorema de Pitágoras para calcular la diagonal del móvil (hipotenusa). El teorema dice:
Y tenemos que sustituir cada letra por las medidas de la pantalla de nuestro teléfono, usando para ello la imagen de arriba:
Luego, realizamos la operación que hemos conseguido. Para eso, primero, elevamos al cuadrado los catetos:
Una vez hecho eso, hacemos la suma:
Y, ahora, quitamos la potencia a la x. Para ello, pasamos el ² al lado derecho de la ecuación. Al pasar una potencia de “elevado a dos: ²” al otro lado, todo lo de ese lado se convierte en una raíz cuadrada (√ ):
Para finalizar, hacemos la raíz cuadrada:
¡Ya hemos averiguado cuánto mide x mediante el Teorema de Pitágoras! Por lo que la diagonal de este teléfono mide 13 cm.
Aplicaciones del teorema de Pitágoras en la vida real
Muchas veces, al aprender un concepto matemático, pensamos: “¿Y esto para qué sirve?”. Pues el Teorema de Pitágoras sirve para mucho más que lo que te imaginas, como por ejemplo:
- Como hemos visto, para calcular el tamaño de la pantalla de tu televisión o móvil. Los smartphones actuales tienen grandes pantallas que se miden en pulgadas en base al cálculo de la diagonal de la pantalla. Para ello se utiliza el Teorema de Pitágoras.
- En la arquitectura o la carpintería, para construir. Por ejemplo, mediante el Teorema de Pitágoras, un arquitecto puede calcular la longitud del tejado de una casa. O también puede calcular el tamaño de los cables que va a necesitar para sostener un puente.
- Para asegurarse de que algo está recto. Según el teorema, un triángulo de 3 m x 4 m x 5 m es un triángulo recto. Por tanto, un triángulo con medidas proporcionales a las descritas será siempre recto. Esta propiedad puede usarse para asegurarse de que, por ejemplo, una pared está recta ¡O incluso para marcar en el suelo un campo de fútbol con líneas rectas entre sí!
- Para localizarte en un mapa. Los teléfonos usan el sistema GPS para efectuar la geolocalización. Ese sistema se basa en el uso de la triangulación, que consiste en determinar una posición en base a otras dos posiciones conocidas. Y ese mismo sistema es utilizado en aviones, barcos ¡O incluso satélites espaciales! Hasta es utilizado para localizar el epicentro de un terremoto. Por lo que, de no ser por el Teorema de Pitágoras, tu teléfono no podría localizarte.
- Para determinar la medida de grandes objetos difíciles de medir como montañas o edificios.
- En una escena de crimen, el teorema de Pitágoras puede usarse para adivinar la trayectoria de la bala del asesino, y, así, saber desde dónde disparó.

